refracion y trasicion de ondas

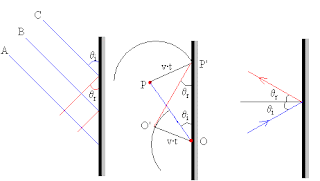
Un movimiento ondulatorio que incide sobre la superficie que separa dos medios de distintas propiedades mecánicas, ópticas, etc., en parte se refleja y en parte se transmite.
La velocidad de propagación de las ondas cambia al pasar de un medio a otro, pero no cambia la frecuencia angular w.
Supongamos que un movimiento ondulatorio se propaga a lo largo de dos cuerdas, la cuerda de la izquierda tiene una densidad lineal m1 y la cuerda de la derecha tiene una densidad lineal m2.

Ley de la reflexión

En la parte izquierda de la figura, se muestra el aspecto de un frente de ondas que se refleja sobre una superficie plana. Si el ángulo que forma el frente incidente con la superficie reflectante es θi, vamos a demostrar, aplicando el principio de Huygens, que el frente de ondas reflejado forma un ángulo θr tal que θi= θr.
Las posiciones del frente de ondas al cabo de un cierto tiempo t, se calculan trazando circunferencias de radio v·t con centro en las fuentes secundarias de ondas situadas en varios puntos del frente de onda inicial.
Las ondas secundarias situadas junto al extremos superior A se propagarán sin obstáculo, su envolvente dará lugar a un nuevo frente de ondas paralelo al inicial y situado a una distancia v·t. Las ondas secundarias producidas en el extremo inferior del frente de ondas chocan contra la superficie reflectante, invirtiendo el sentido de su propagación. La envolvente de las ondas secundarias reflejadas da lugar a la parte del frente de ondas reflejado. El frente de ondas completo en el instante t tiene la forma de una línea quebrada.
Tomemos la fuente de ondas secundarias P, de la porción OP del frente de ondas incidente, trazamos la recta perpendicular PP’, tal que PP’=v·t. Con centro en O trazamos una circunferencia de radio v·t. Se traza el segmento P’O’ que es tangente a dicha circunferencia. Este segmento, es la porción del frente de ondas reflejado. De la igualdad de los triángulos OPP’ y OO’P’ se concluye que el ángulo θi es igual al ángulo θr.
Si trazamos las rectas perpendiculares (denominadas rayos) a los frentes de onda incidente y reflejado, se concluye, que el ángulo de incidencia θi formado por el rayo incidente y la normal a la superficie reflectante, es igual al ángulo de reflexión θr formado por el rayo reflejado y dicha normal.

Superposición de ondas

En la mecánica ondulatoria la interferencia es lo que resulta de la superposición de dos o más ondas, resultando en la creación de un nuevo patrón de ondas. Aunque la acepción más usual para interferencia se refiere a la superposición de dos o más ondas de frecuencia idéntica o similar.
El principio de superposición de ondas establece que la magnitud del desplazamiento ondulatorio en cualquier punto del medio es igual a la suma de los desplazamientos en ese mismo punto de todas las ondas presentes. Esto es consecuencia de que la Ecuación de onda es lineal, y por tanto si existen dos o más soluciones, cualquier combinación lineal de ellas será también solución.
Si la cresta de una onda se produce en el punto de interés mientras la cresta de otra onda también arriba a ese punto (es decir, si ambas ondas están en fase), ambas ondas se interferirán constructivamente, resultando en una onda de mayor amplitud.