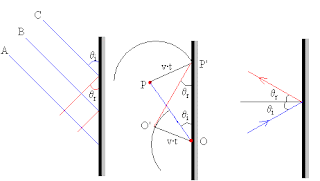
El principio de Huygens es un método de análisis aplicado a los problemas de propagación de ondas. Reconoce que cada punto de un frente de onda que avanza es de hecho el centro de una nueva perturbación y la fuente de un nuevo tren de ondas; y que la onda que avanza como un todo se puede mirar como la suma de todas las ondas secundarias que surgen de puntos en el medio ya atravesado. Las ondas resultantes se convierten en un frente de ondas que avanza en la misma dirección que el que la generó y cada nuevo frente de onda es suceptible a su vez de ser núcleo de un nuevo frente de ondas.

Esta visión de la propagación de las ondas ayuda a entender mejor una variedad de fenómenos de onda, tales como la difracción. La Ley de Snell también puede ser explicada según este principio.Esta visión de la propagación de las ondas ayuda a entender mejor una variedad de fenómenos de onda, tales como la difracción. La Ley de Snell también puede ser explicada según este principio.
Por ejemplo, si dos sitios están conectados por una puerta abierta y se produce un sonido en una esquina lejana de uno de ellos, una persona en el otro cuarto oirá el sonido como si se originara en el umbral. Por lo que se refiere el segundo cuarto, el aire que vibra en el umbral es la fuente del sonido. Lo mismo ocurre para la luz al pasar el borde de un obstáculo, pero esto no es fácilmente observable debido a la corta longitud de onda de la luz visible. La interferencia de la luz de áreas con distancias variables del frente de onda móvil explica los máximos y los mínimos observables como franjas de difracción. Ver, por ejemplo, el experimento de dos rendijas.
Christiaan Huygens ['krɪstja:n 'hœyxəns](14 de abril de 1629 - 8 de julio de 1695) fue un astrónomo, físico y matemático holandés, nacido en La Haya.
Astronomía
Aficionado a la astronomía desde pequeño, pronto aprendió a tallar lentes (especialidad de Holanda desde la invención del telescopio, hacia el año 1608) y junto a su hermano Constantin llegó a construir varios telescopios de gran calidad. Por el método de ensayo y error comprobaron que los objetivos de gran longitud focal proporcionaban mejores imágenes, de manera que se dedicó a construir instrumentos de focales cada vez mayores: elaboró un sistema especial para tallar este tipo de lentes, siendo ayudado por su amigo el filósofo Spinoza, pulidor de lentes de profesión. El éxito obtenido animó a Johannes Hevelius a fabricarse él mismo sus telescopios.
En 1655 terminó un telescopio de gran calidad: apenas tenía 5 cm de diámetro aunque medía más de tres metros y medio de longitud, lo que le permitía obtener unos cincuenta aumentos: con este aparato descubrió que en torno al planeta Saturno existía un anillo (visto por otros astrónomos anteriores pero no identificado claramente) y la existencia de un satélite, Titán, el 25 de marzo de ese año. Después de seguirlo durante varios meses, para estar seguro de su período y órbita, dio a conocer la noticia en 1656.
Realizó importantes descubrimientos en el campo de la astronomía gracias a la invención de una nueva lente ocular para el telescopio. Estudió la Nebulosa de Orión (conocida también como M42), descubriendo que en su interior existían estrellas diminutas. En 1658 diseñó un micrómetro para medir pequeñas distancias angulares, con el cual pudo determinar el tamaño aparente de los planetas o la separación de los satélites planetarios.